Sommaire :
Qui est Archimède ? Le mathématicien a expliqué le phénomène scientifiquement
Archimède c’est un scientifique grec. Alors à l’époque un scientifique est souvent tout à la fois ingénieur, physicien, mathématicien etc… Un peu comme Pythagore qui était aussi philosophe et dont nous parlions dans un article précédent.
Alors notez que, si comme pour Pythagore, nous ne sommes pas sûr de l’année de naissance d’Archimède (environ 287 avant Jésus-Christ), nous n’avons pas non plus beaucoup d’informations sur sa vie privée. On sait qu’il a vécu à Syracuse en Sicile et qu’il y est mort en 212 avant Jésus-Christ. Comment ? Tué par un soldat romain pendant le siège de Syracuse, alors qu’il avait été donné l’ordre de l’épargner, c’est ballot… d’autant qu’on ne s’en prend pas à un si brillant cerveau ! Quand on le peut, on le récupère ! C’est donc surtout son héritage scientifique qui a marqué l’histoire.

C’est un des plus grands mathématiciens de tous les temps, et sa production scientifique nous parvient principalement grâce à ce que l’on a pu retrouver de ses écrits, dont certains sont encore en cours de déchiffrage (oui oui, les progrès de la technique permettent d’analyser aujourd’hui de vieux documents abîmés et d’y découvrir des choses que nous étions encore incapables d’observer il y a à peine quelques années).
Je ne vais pas m’étendre sur ce qu’il nous lègue, sinon je vais encore partir sur un article long comme le bras. Non je vais surtout faire un agrandissement sur son fameux « principe » !
Le principe d’Archimède
La légende : épisode 1 / 2
Hiéron II, qui règne alors sur Syracuse, le charge de déterminer si la couronne qu’il a faite faire chez un orfèvre est bien en or massif, et ce bien sûr sans la détériorer (donc sans la fondre ou la couper pour voir ce qu’elle contient). Archimède n’aurait alors que 22 ans, et il est déjà l’ami et le conseiller scientifique du roi !
Alors comment faire ? La couronne a une forme compliquée, il est donc très difficile de calculer son volume avec une règle, pour ensuite vérifier que son poids correspond bien au volume d’or qu’elle contient…
La légende veut que c’est en prenant son bain, et en constatant qu’en entrant dans le bain le niveau de l’eau était monté, qu’Archimède aurait trouvé un moyen de répondre à la question d’Hérion. Il s’écria alors son fameux « Eurêka ! » (qui en grec veut juste dire « j’ai trouvé »… en fait – c’est moins épique une fois traduit hein ).
L’explication scientifique du principe
« Tout corps plongé dans un fluide reçoit de la part de ce fluide une force (poussée) verticale, vers le haut dont l’intensité est égale au poids du volume de fluide déplacé ».
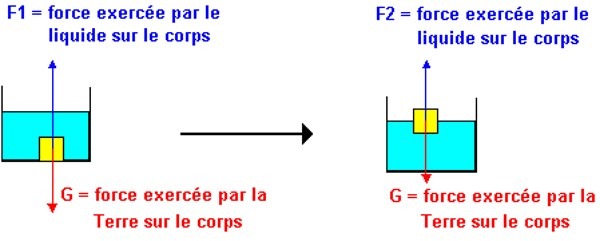
En clair ? Si vous immergez complètement un ballon d’un litre dans de l’eau, eh bien vous déplacez 1 litre d’eau. Jusque là on est d’accord. Ce litre d’eau déplacée par le ballon pèse environ 1 kilogramme, donc le ballon subira une poussée en direction de la surface de 1 kilogramme. Donc s’il est suffisamment léger (par exemple un ballon de foot pèse moins de 450 grammes pour environ 1,750 litre) et que vous le lâchez, cette poussée va le faire remonter vers la surface.
Plus globalement, la poussée d’Archimède est une force que subit un corps plongé dans un fluide (liquide ou gaz) soumis à un champ de gravité et donc à la pression liée à son propre poids. L’augmentation de la pression du fluide avec la profondeur (effet de la gravité sur le fluide) fait que la pression est plus forte au bas de l’objet que sur le haut de l’objet, donc la poussée qui en résulte est orientée vers le « haut », en sens inverse de la gravité qui s’exerce sur le fluide, et est égale au poids du volume du fluide déplacé par l’objet immergé.
Découverte de la poussée d’Archimède : ça à l’air de bien le faire kiffer lui aussi
La légende : épisode 2 / 2
Fort de ce principe, Archimède plonge la couronne dans l’eau, observe quel volume d’eau à été déplacé, et en déduit le volume de la couronne.
Ensuite il pèse la couronne, et connaissant la masse volumique de l’or (c’est à dire le poids de l’or en fonction de son volume), il peut vérifier si le poids de la couronne correspond bien au poids d’un volume d’or équivalent ! Et là patatras… il n’y a visiblement pas que de l’or dans la couronne.
Et là vous me direz : oui mais ça ne fait pas intervenir le principe d’Archimède ? On ne parle pas de « poussée »… Vous avez raison, la légende raconte que c’est comme ça qu’est né son fameux principe, en cherchant une solution au problème. Par contre il n’a pas eu besoin de son principe pour résoudre le problème.
Et là vous me direz : le volume d’une couronne est très petit, franchement la plonger dans l’eau pour en mesurer le volume n’a pas pu donner un résultat assez précis pour déterminer si c’était bien de l’or massif. Je vous avoue qu’il s’y est peut-être pris différemment de ce qu’on raconte, et que votre point est pertinent. Enfin qui sait, il s’est peut être vachement appliqué ! Et la légende est assez cool.
Pourquoi les bateaux flottent ?
Pour la même raison que les montgolfières décollent ! Le fameux principe d’Archimède.
Un bateau, même en fer, a une coque qui déplace beaucoup beaucoup d’eau. Comme la coque est en partie vide (enfin, remplie d’air) et que l’air est beaucoup plus léger que l’eau, la poussée équivalente au poids du volume d’eau déplacé est de plus en plus grande au fur et à mesure que la coque s’enfonce dans l’eau, jusqu’à s’équilibrer avec le poids de la coque et que le bateau flotte. Et plus on charge le bateau, plus la coque s’enfonce dans l’eau et plus elle déplace d’eau, donc plus la poussée d’Archimède verticale est importante. Il y a simplement un équilibre qui se fait entre l’eau déplacée quand le bateau s’y enfonce sous son propre poids, et la poussée d’Archimède qui augmente à mesure que le bateau s’enfonce.
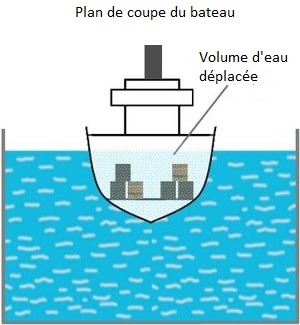
Bon si vous faites un trou dans la coque et que de l’eau rentre… la masse volumique du bateau se rapproche furieusement de celle de l’eau qui l’entoure, en plus de la masse volumique du fer qui est bien supérieure à celle de l’eau, au global la masse volumique du bateau finit par dépasser celle de l’eau qui l’entoure et… il coule.
Idem pour les montgolfières !
Le ballon est rempli d’air chaud. Or l’air est en quelque sorte « dilaté » par la chaleur, c’est à dire qu’une même masse d’air occupe un volume plus important. On peut donc dire qu’avec la chaleur, la masse volumique de l’air diminue. Le ballon est donc gonflé d’un air chaud qui, à volume égal avec l’air froid, est plus léger que l’air froid. Donc la poussée d’Archimède exercée par l’air froid extérieur et dense, sur le volume du ballon, est plus importante que le poids en air chaud contenu dans le ballon. Voilà pourquoi le ballon décolle !
Et là vous allez me dire : « oui mais quand le ballon prend de l’altitude, la pression atmosphérique diminue et la densité de l’air aussi. Du coup la poussée d’Archimède sur le ballon diminue… alors au delà d’une certaine altitude, le ballon retombe ?
Wow, vous posez de sacrément bonnes questions aujourd’hui ! Comment vous répondre… disons qu’en effet le ballon arrête de monter quand la densité de l’air devient trop petite. Ou alors il monte encore un peu, juste avec son élan, et puis il redescend un peu jusqu’à-ce que à nouveau la poussée d’Archimède soit plus grande que le poids du ballon et ainsi de suite, bref, il oscille doucement et faiblement autours de son point d’équilibre, à l’altitude où la densité de l’air extérieur (qui provoque la poussée d’Archimède) s’égalise, s’équilibre avec la densité de l’air à l’intérieur du ballon (qui donne un poids au ballon, en plus de la nacelle, des passagers, de l’enveloppe du ballon, des brûleurs bref… l’ensemble des éléments qui font le poids du ballon).












Leave a Reply